Bayes統計による推論
目次
ベイズ統計学
Aを理論モデル、Bを観測データとした場合に、条件付き確率に対する次の等式を利用して、与えられたデータに基づいて理論モデルについて推論することができる。
P(A|B) = P(B|A)*P(A)/P(B)
通常は、理論モデルAがあったとき、そこからデータBを得る確率P(B|A)を計算することが(原理的には)できる。一方、観測であるデータBを得たときに、そのような結果を引き起こすモデルとしてどのようなものが適当かという問いは自明ではない。あらゆるモデルを考えたのでは範囲が広すぎるが、あるモデルを考えたときに、そのモデルのパラメータを推論するというのは取り扱いが可能である。理論モデルから観測結果を予測するという順問題に対して、観測されたデータから理論モデルの妥当性やパラメータを決定するという逆問題への一つのアプローチである。
課題
確率分布と確率事象の生成・描画
Pythonを使ったデータ解析と描画の練習。Pythonのモジュール(numpy, matplotlib.pyplot, scipy)を利用するのでインストールしておく。
sudo pip3 install numpy matplotlib scipy
- randomモジュールを使って一様分布やガウス分布に従うデータを生成して分布をヒストグラムにして確認する。また、ガウス分布の関数形を一緒に表示させる。
- 2つの確率変数(x1, x2)を多数生成して、それらの相関を表示させる。横軸にx1, 縦軸にx2を取った相関図
- ガウス分布に従う乱数で生成したヒストグラムをガウス分布でフィットする
データを基にしたモデル・パラメータのベイズ推定
ガウス分布にしたがって生成された事象から、元の確率分布の平均と標準偏差をベイズ法によって求める。
P(p|x) = P(x|p)*P(p)
- パラメータの事前確率分布P(p)を一様分布と仮定する
- Likelihood関数P(x|p)を知っているものとする
- この2つの量からパラメータについて、様々な値に対して右辺の値を計算する
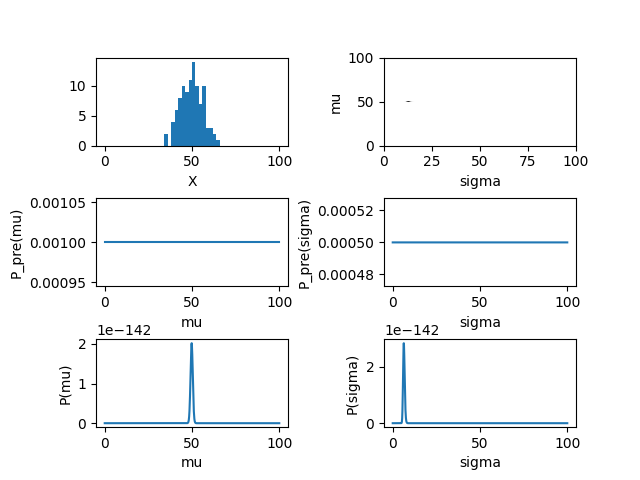
この手順を事象数がN=2, 10, 100の場合について実行したものが以下の図である。データはmu=50, sigma=6.0として生成した。 上左の図が生成された変数の分布、2段目の図は平均と標準偏差の事前分布(一様分布)、下段は平均と標準偏差の事後分布である。データの事象数が増えるにしたがって、事後分布が鋭くなっていく様子が分かる。
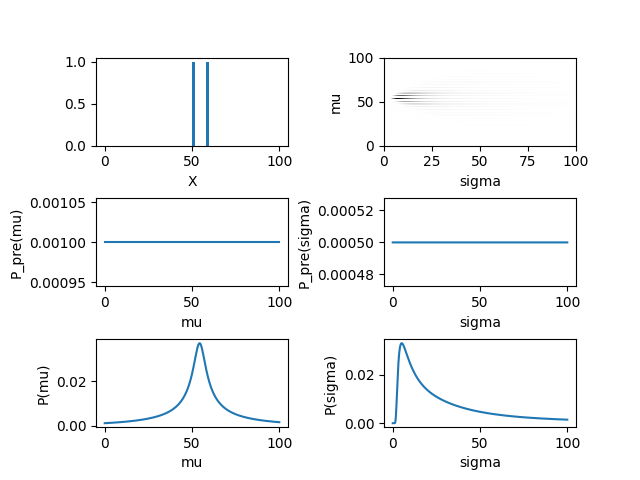 ,
, 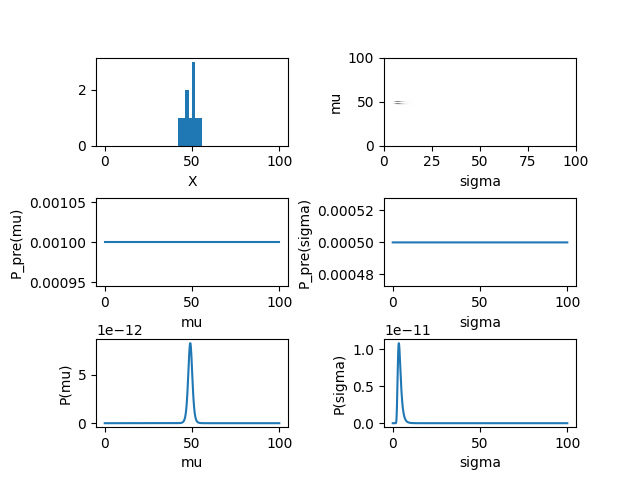 ,
, 
コードは githubへのリンクにある。
簡単な問題への適用
2重スリット実験における光学系のセットアップの推定
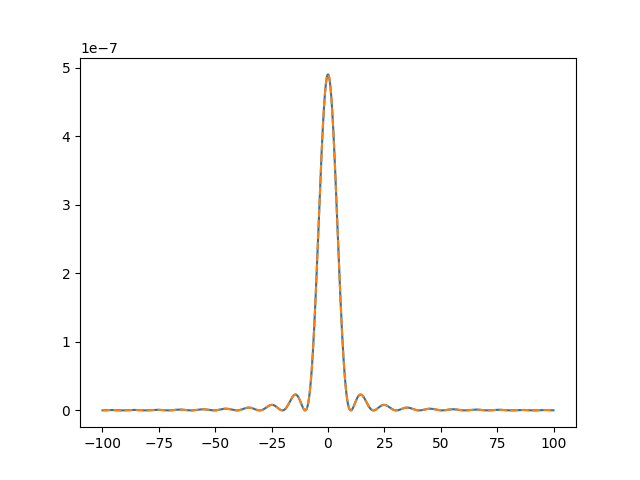
画像の復元
ノイズやぼかしの入った画像を復元できるか試す。 LinuxUsageAdvanced#ProjectStructureを参考に作業環境を用意する。
ソースコードのダウンロードとコンパイルの手順は以下の通りである。
cd WORKAREA/projectA source ./scripts/setup.sh cd dev git clone https://github.com/tkono17/labpp.git mkdir build cd build cmake ../labpp/Setups/bayesStat make install
これで、Pythonのコードが$SWDIR以下にインストールされるはずである。
ls $SWDIR/bin ls $SWDIR/python which blurImage.py
と実行して、ファイルがインストール先にコピーされているか、実行可能プログラムが見つかるか確認する。
画像をぼかす、または復元するプログラムblurImage.pyの実行の仕方はdev/labpp/Statistics/Bayes/scripts/run_blurImage.shにあるので、このファイルを自分の作業場所にコピーして使う。 画像は、まずは写真よりもイラストの方が分かりやすいと思うので、自分で描くかpixabay.com等の素材サイトから無料画像をダウンロードして使える。
